1D Cochlear Models¶
by Liu-Jie Ren
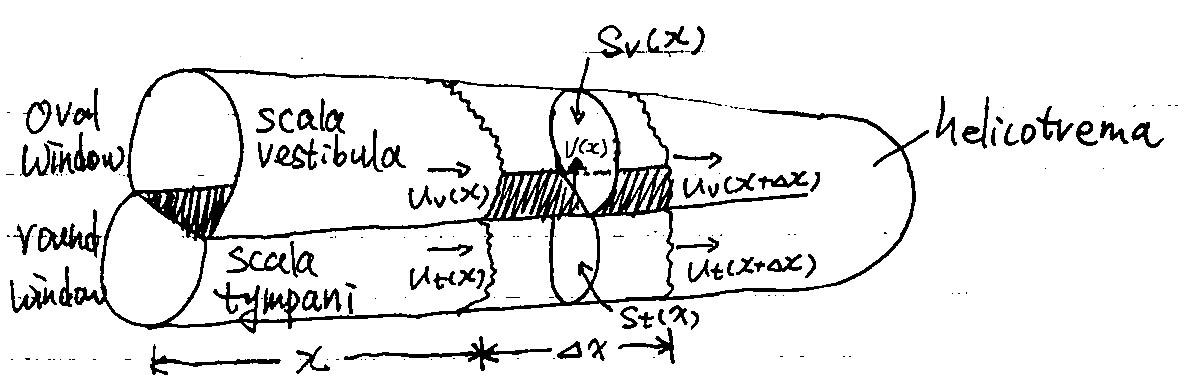
Notations
$v(x,t)$ - the velocity of the basilar membrane; $b(x)$ - the width of the basilar membrane; $S_v(x,t), S_t(x,t)$ - section area of the scala vestibula and scala tympani, respectively; $\rho(x,t)$ - fluid density; $p_v(x,t), p_t(x,t)$ - pressure of the two scalae; $c$ - sound speed in the fluid; $u_v(x,t), u_t(x,t)$ - fluid velocity at the two scalae.
Control equation in general¶
Mass conservation¶
We use basic fluid dynamics to describe the problem, let's first consider a cross section from $x$ to $x+\Delta x$, over a time period $t\rightarrow t+\Delta t$. For the scala vestibula (the upper chamber), we have:
- Mass flow into the section: $\Delta M_1 = \rho(x,t) \cdot u_v(x,t) S_{v}(x,t) \Delta t$
- Mass flow out of the section: $\Delta M_2 = \rho(x,t) \cdot u_v(x+\Delta x,t) S_{v}(x+\Delta x,t) \Delta t$
- Equavilent mass flow in from the basilar membrane $\Delta M_3 = \rho(x,t) \cdot v(x,t)b(x)\Delta x\Delta t$
- Mass change of the section over time $t$ to $t+\Delta t$
- the initial mass: $\rho(x,t)S_v(x,t)\Delta x$
- mass at time $t+\Delta t$: $\rho(x,t+\Delta t)S_v(x,t+\Delta t)\Delta x$
- the mass change: $\Delta M_4 = \left[ \rho(x,t+\Delta t)S_v(x,t+\Delta t)-\rho(x,t)S_v(x,t) \right]\Delta x$
According to mass conservation, we have $\Delta M_1-\Delta M_2+\Delta M_3 = \Delta M_4$, that is $$ \rho u_v S_v \Delta t - \rho u_v(\Delta x) S_v(\Delta x) \Delta t + \rho bv\Delta x\Delta t = \Delta x\left( \rho(\Delta t)S_v(\Delta t)-\rho S_v\right)$$ Here we simplify $A(x,t)$ as $A$, $A(x,t+\Delta t)$ as $A(\Delta t)$, and $A(x+\Delta x,t)$ as $A(\Delta x)$, then we have
$$\frac{1}{\rho}\frac{\partial(\rho S_v)}{\partial t} + \frac{\partial (S_v u_v)}{\partial x} - b v = 0$$Similarly, for the scala tympani, we have $$\frac{1}{\rho}\frac{\partial(\rho S_t)}{\partial t} + \frac{\partial (S_t u_t)}{\partial x} + b v = 0$$
Comment: The above equations include the effect of density change (thus the fluid is compressible), the shape change of the section (thus $S_v$ and $S_t$ are time-dependent, which is only considerable in bone conduction).
Momentum equation¶
Let's consider the momentum equation, accroding to Navier-Stokes equation for invicid flow, ingoring convection term and body force, we have $\rho\frac{\partial \vec{u}}{\partial t}=-\nabla p$, in $x-$direction, we have $\rho\frac{\partial u_v}{\partial t}=-\frac{\partial p_v}{\partial x}$ and $\rho\frac{\partial u_t}{\partial t}=-\frac{\partial p_t}{\partial x}$.
Sound speed¶
The mass conservation equation can be simplified, and we try to cancel out the term $\partial \rho/\partial t$. Consider the fluid as slightly compressible, we have the relation $$ \frac{\partial p}{\partial \rho} = c^2 $$ where $c$ is sound speed in the fluid. Thus for the scala vestibula, we have $$ \begin{align} \frac{1}{\rho}\frac{\partial(\rho S_v)}{\partial t} + & \frac{\partial (S_v u_v)}{\partial x} - b v = 0 \\ \longrightarrow & \frac{\partial S_v}{\partial t}+\frac{S_v}{\rho}\frac{\partial \rho}{\partial t}+\frac{\partial (S_v u_v)}{\partial x}- b v = 0 \\ \longrightarrow & \boxed{ \frac{\partial S_v}{\partial t}+\frac{S_v}{\rho c^2}\frac{\partial p_v}{\partial t}+\frac{\partial (S_v u_v)}{\partial x}- b v = 0 }\\ \end{align} $$ Similarly, for the scala tympani, we have $$ \boxed{ \frac{\partial S_t}{\partial t}+\frac{S_t}{\rho c^2}\frac{\partial p_t}{\partial t}+\frac{\partial (S_t u_t)}{\partial x}+ b v = 0} $$
Boundary conditions¶
We can add several boundary conditions to the model
- The velocity and pressure relation at the oval window, we have $\rho \frac{\partial u_v(x=0)}{\partial t}=-\frac{\partial p_v(x=0)}{\partial x}$, or we can simply define $p_v(x=0)$;
- The velocity and pressure relation at the round window, we have $\rho \frac{\partial u_t(x=0)}{\partial t}=-\frac{\partial p_t(x=0)}{\partial x}$, or more often, we simply let $p_t(x=0)=0$;
- The helicotrema: since the two scalae connect each other, we have $p_v(L) = p_t(L)$, where $L$ is the basilar membrane length.
Dynamics for the basilar membrane¶
For a 1-DOF basilar membrane model, the control equation is $$ k(x,t)\eta(x,t)+r(x,t)\dot{\eta}(x,t)+m(x,t)\ddot{\eta}(x,t) = -(p_v(x,t)-p_t(x,t)) $$ where $k$, $r$ and $m$ are the stiffness, damping and mass, $\eta$ is the BM displacement, satisfying that $\dot{\eta}=v$.
Peterson and Bogert, 1950¶
This section review the work by Peterson and Bogert (1950).
Peterson L C, Bogert B P. A dynamical theory of the cochlea[J]. The Journal of the Acoustical Society of America, 1950, 22(3): 369-381.
Theoretical simplifications¶
Several assumptions were added to simplify the model, as follows
- We are talking about air conduction, thus the cochlea wall will not deform and the section area keeps unchanging: $\partial{S_v}/\partial t = \partial{S_t}/\partial t=0$.
- Consider the geometrical symmetry of the two scala, thus $S_v(x)=S_t(x)=S_0(x)$.
- Although the section can be varing along the cochlea length, but the shape is rather smooth, thus $\partial{S_0}/\partial x\approx 0$.
Thus we have $$\begin{align} &\boxed{ \frac{\partial(S_0 u_v)}{\partial x} + \frac{S_0}{\rho c^2}\frac{\partial p_v}{\partial t} = bv} \\ &\boxed{ \frac{\partial(S_0 u_t)}{\partial x} + \frac{S_0}{\rho c^2}\frac{\partial p_t}{\partial t}= -bv} \end{align}$$
Now let's consider the scala vestibula, we have $$\begin{align} \frac{\partial u_v}{\partial x} + \frac{1}{\rho c^2}\frac{\partial p_v}{\partial t} = \frac{bv}{S_0} &\longrightarrow \frac{\partial^2 u_v}{\partial x\partial t} + \frac{1}{\rho c^2}\frac{\partial^2p_v}{\partial t^2} = \frac{b\dot{v}}{S_0} \\ \rho\frac{\partial u_v}{\partial t} = -\frac{\partial p_v}{\partial x} &\longrightarrow \frac{\partial^2 u_v}{\partial t\partial x} = -\frac{1}{\rho}\frac{\partial^2 p_v}{\partial x^2} \end{align}$$ $$ \boxed{ \frac{\partial^2p_v}{\partial t^2} - c^2\frac{\partial^2 p_v}{\partial x^2} = \frac{\rho c^2 b\dot{v}}{S_0} } $$ and similarly, $$ \boxed{ \frac{\partial^2p_t}{\partial t^2} - c^2\frac{\partial^2 p_t}{\partial x^2} =-\frac{\rho c^2 b\dot{v}}{S_0} } $$
Assume that $p_+=\frac{1}{2}(p_v+p_t)$ and $p_-=\frac{1}{2}(p_v-p_t)$, we have $$ \boxed{ \frac{\partial^2p_+}{\partial t^2} - c^2\frac{\partial^2 p_+}{\partial x^2} = 0 }$$ which traveling in the speed of sound, and $$ \boxed{ \frac{\partial^2p_-}{\partial t^2} - c^2\frac{\partial^2 p_-}{\partial x^2} = \frac{\rho c^2 b\dot{v}}{S_0} }$$ Remember that $k(x,t)\eta(x,t)+r(x,t)\dot{\eta}(x,t)+m(x,t)\ddot{\eta}(x,t) = −2p_-$
Harmonic solutions in the frequency domain¶
Consider the solutions in the frequency domain, let $p_-(x,t)=P(x)\exp(j\omega t)$, we have $$ \frac{\omega^2}{c^2} P + \frac{\partial^2 P}{\partial x^2} = \frac{\rho b \omega^2}{S_0} \eta$$ and $$ ( k-m\omega^2+j\omega c) \eta = Y(x)\eta = -2P $$ Thus $$ \boxed{ \frac{\partial^2 P}{\partial x^2} = \left(-\frac{2 \rho b \omega^2}{S_0 Y(x)}-\frac{\omega^2}{c^2} \right) P } $$
Parameters (SI units)¶
- We assume that $x\in [0, 3.5]$ cm $\longrightarrow x=[0, 0.035]$.
- $S_0(x) = 0.029-0.005x$cm$^2$ $\longrightarrow S_0(x)= (0.029-0.5x)\times 10^{-4} $
- $b(x) = 0.019+0.0093x$cm $\longrightarrow b(x)= (0.019+0.93x)\times 10^{-2} $
- $k(x) = 1.72\times 10^9 \exp(-2x)$ dyne/cm$^3$ $\longrightarrow k(x) = 1.72\times 10^{10} \exp(-200x)$
- $m(x) = 0.143$g/cm$^2$ $\longrightarrow m(x)=1.43$
- $\rho = 1, c = 1430$
- $P(0) = 1, P(L) = 0$
Finite difference¶
$$ \boxed{ \frac{P_{k-1}+P_{k+1}-2P_k}{\Delta x^2} = \left(-\frac{2 \rho b \omega^2}{S_0 Y_k}-\frac{\omega^2}{c^2} \right) P_k }$$%%file cochlea_model_1d_peterson.m
function cochlea_model_1d_peterson(frequency)
N = 401;
L = 0.035;
x = linspace(0,L,N)';
S0 = 1e-4*(0.029-0.5*x);
b = 1e-2*(0.019+0.93*x);
k = 1.72e10*exp(-200*x);
m = 1.43;
r = 2*0.02*sqrt(k*m);
rho = 1000;
c = 1430;
for freq = frequency
w = 2*pi*freq;
Y = k-m*w.^2+1i*w*r;
% finite difference
K = zeros(N,N); F = zeros(N,1); dx = L/(N-1);
for ii = 2:N-1
K(ii,ii-1) = -1;
K(ii,ii+1) = -1;
K(ii,ii) = 2-dx*dx*w*w*(2*rho*b(ii)/S0(ii)/Y(ii)+1/c^2 );
end
K(1,1) = 1; F(1) = 1;
K(N,N) = 1; F(N) = 0;
P = K\F;
y = -2*P./Y;
% rho*du/dt = -dp/dx ==> -rho w^2 Us = [ p(1)-p(2) ] / dx
Us = ( P(1)-P(2) )/dx/(-rho*w^2);
y0 = y;
y = y./Us;
figure(1);
subplot(1,3,1); hold on; grid on;
plot(x, real(P), 'r-', 'linewidth', 2);
plot(x, abs(P), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('pressure difference');
set(gca,'xlim',[0,L]);
subplot(1,3,2); hold on; grid on;
plot(x, real(y), 'r-', 'linewidth', 2);
plot(x, abs(y), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('BM displacement re stapes');
set(gca,'xlim',[0,L]);
subplot(1,3,3); hold on; grid on;
plot(x, 20*log10( abs(y) ), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('BM displacement amp. in dB');
set(gca,'xlim',[0,L]);
fprintf(1,'frequency: %6d Hz, maximum BM disp. %e , velo. %e \n',...
freq, max(abs(y0)), max(abs(1i*w*y0)) );
end
end
%plot inline --size 1200,300
cochlea_model_1d_peterson([1000,3160,10000]);
The same model was used by Zwislocki 1950
Zwislocki J. Theory of the acoustical action of the cochlea[J]. The Journal of the Acoustical Society of America, 1950, 22(6): 778-784.
Issues of 1D models¶
- to get correct CF (characteristic frequency 20~20k), the BM stiffness should vary by 4~6 orders, which is not the truth;
- the fast wave $P_+$ are not significant at least below 7000 Hz, thus many models assume the fluid incompressible;
- a passive model cannot mimic well at the CF location, where the wavelength is rather "short".
Attempt of Nonlinear Passive Models¶
Hubbard and Geisler (1972)¶
The group developed the first non-linear cochlea model using nonlinear damping.
Hubbard A E, Geisler C D. A Hybrid‐Computer Model of the Cochlear Partition[J]. The Journal of the Acoustical Society of America, 1972, 51(6B): 1895-1903.
The method used in the article is old, now we have better computation enviroment, thus we propose a new nonlinear damping assumption: $ \displaystyle r(x) = \frac{1}{1+e^{-a(\lg|\eta| -b)}} $, in this model, we assume $a=2$ and $b=-8$, and we scale the damping to [0.01,0.3]. That is, the damping at location $x$ is decided by the local BM displacement amplitude $|\eta(x)|$.
%plot inline --size 500,200
eta = 10.^linspace(-10,-6,101)';
a = 2; b = -8;
r = 0.01+ 0.29./(1+exp( -a*(log10(eta)-b)) );
plot(eta,r,'k-','linewidth',2);
set(gca,'xscale','log','ylim',[0,0.35]);
xlabel('BM displacement, \eta');
ylabel('local damping');
grid on;
title('Nonlinear damping relation to BM displacement');
%%file cochlea_model_1d_nonlinear_damping.m
function cochlea_model_1d_nonlinear_damping(freq,P0)
N = 401;
L = 0.035;
x = linspace(0,L,N)';
S0 = 1e-4*(0.029-0.5*x);
b = 1e-2*(0.019+0.93*x);
k = 1.72e10*exp(-200*x);
m = 1.43;
damping = 0.02*ones(N,1);
r = 2*damping.*sqrt(k*m);
rho = 1000;
c = 1430;
error = 1;
for steps = 1:1000
w = 2*pi*freq;
r = 2*damping.*sqrt(k*m);
Y = k-m*w.^2+1i*w*r;
% finite difference
K = zeros(N,N); F = zeros(N,1); dx = L/(N-1);
for ii = 2:N-1
K(ii,ii-1) = -1;
K(ii,ii+1) = -1;
K(ii,ii) = 2-dx*dx*w*w*(2*rho*b(ii)/S0(ii)/Y(ii)+1/c^2 );
end
K(1,1) = 1; F(1) = P0;
K(N,N) = 1; F(N) = 0;
P = K\F;
y = -2*P./Y;
% rho*du/dt = -dp/dx ==> -rho w^2 Us = [ p(1)-p(2) ] / dx
Us = ( P(1)-P(2) )/dx/(-rho*w^2);
y0 = y;
y = y./Us;
% revise damping
damping1 = 0.01+0.29./(1+exp( -2*(log10(abs(y0))+8)) );
error = max(abs((damping1-damping)./damping1));
if error<0.01
break;
end
damping = damping1;
end
figure(1);
subplot(2,2,1); hold on; grid on;
plot(x, 28*log10(abs(P)), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('pressure difference in dB');
set(gca,'ylim',[-150,50]);
subplot(2,2,2); hold on; grid on;
plot(x, real(y), 'r-', 'linewidth', 2);
plot(x, abs(y), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('BM displacement re stapes');
subplot(2,2,3); hold on; grid on;
plot(x, 20*log10( abs(y) ), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('BM displacement amp. in dB');
set(gca,'ylim',[-30,40]);
subplot(2,2,4); hold on; grid on;
plot(x, damping, 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('damping coefficients');
fprintf(1,'frequency: %6d Hz, maximum BM disp. %e, damping error %f \n', freq, max(abs(y0)),error );
end
%plot inline --size 1200,600
cochlea_model_1d_nonlinear_damping(1000,10);
cochlea_model_1d_nonlinear_damping(1000,1);
cochlea_model_1d_nonlinear_damping(1000,0.1);
cochlea_model_1d_nonlinear_damping(1000,0.01);
cochlea_model_1d_nonlinear_damping(5000,10);
cochlea_model_1d_nonlinear_damping(5000,1);
cochlea_model_1d_nonlinear_damping(5000,0.1);
cochlea_model_1d_nonlinear_damping(5000,0.01);
As we can see, the model present some active/nonlinear properties, that is, at low input level, the cochlea is most sensitive; and at high input level, the system has larger damping and the BM displacement is limited.
Another nonlinear damping model was proposed by Pfeiffer et al. (1973). But the model only contain the BM mechanics (using a second-order differntial equation) and no fluid domain were accounted.
Kim D O, Molnar C E, Pfeiffer R R. A system of nonlinear differential equations modeling basilar‐membrane motion[J]. The Journal of the Acoustical Society of America, 1973, 54(6): 1517-1529.
Hall (1974)¶
Hall (1974) also use the nonlinear damping as $\displaystyle r = r_0 (1+\alpha v +\beta v^2)$ where $r$ is the damping, $v$ is the velocity of the BM.
Hall J L. Two‐tone distortion products in a nonlinear model of the basilar membrane[J]. The Journal of the Acoustical Society of America, 1974, 56(6): 1818-1828.
Hall J L. Two‐tone suppression in a nonlinear model of the basilar membrane[J]. The Journal of the Acoustical Society of America, 1977, 61(3): 802-810.
Hall J L. Spatial differentiation as an auditory’’second filter’’: Assessment on a nonlinear model of the basilar membrane[J]. The Journal of the Acoustical Society of America, 1977, 61(2): 520-524.
They used the model to study two-tone distortion, the term $\alpha v$ is responsible for even distortion products (0Hz, $f_2-f_1$, etc.), and the term $\beta v^2$ is responsible for odd ones ($2f_1-f_2, 2f_2-f_1$, etc.)
%plot inline --size 500,200
v = linspace(-4,4,1001)';
r0 = 1;
a = 0.0316; b = 0.1;
r = r0*(1+a*v+b*v.^2);
plot(v,r,'k-','linewidth',2);
set(gca,'yscale','log');
xlabel('BM displacement, \eta');
ylabel('local damping');
grid on;
title('Nonlinear damping relation to BM displacement');
To study DP, the nonlinear model was simulated by representing the model as a time-varying sampled-data system.
Other models¶
Furst et al. (1982), Hubbard (1986) also assumed that the damping is related with BM velocity. Moreover, they assumed that the stiffness also a function of BM velocity.
Furst M, Goldstein J L. A cochlear nonlinear transmission‐line model compatible with combination tone psychophysics[J]. The Journal of the Acoustical Society of America, 1982, 72(3): 717-726.
Hubbard A E. Cochlear emissions simulated using one-dimensional model of cochlear hydrodynamics[J]. Hearing research, 1986, 21(1): 75-81.
Following is a model that $ \displaystyle r(x) = \frac{1}{1+e^{-a(\lg|v| -b)}} $, in this model, we assume $a=2$ and $b=-4$, and we scale the damping to [0.01,0.3]. That is, the damping at location $x$ is decided by the local BM displacement amplitude $|v(x)|$.
%plot inline --size 500,200
eta = 10.^linspace(-6,-2,101)';
a = 2; b = -4;
r = 0.01+ 0.29./(1+exp( -a*(log10(eta)-b)) );
plot(eta,r,'k-','linewidth',2);
set(gca,'xscale','log','ylim',[0,0.35]);
xlabel('BM velocity, v');
ylabel('local damping');
grid on;
title('Nonlinear damping relation to BM velocity');
%%file cochlea_model_1d_nonlinear_damping_velocity.m
function cochlea_model_1d_nonlinear_damping_velocity(freq,P0)
N = 401;
L = 0.035;
x = linspace(0,L,N)';
S0 = 1e-4*(0.029-0.5*x);
b = 1e-2*(0.019+0.93*x);
k = 1.72e10*exp(-200*x);
m = 1.43;
damping = 0.02*ones(N,1);
r = 2*damping.*sqrt(k*m);
rho = 1000;
c = 1430;
error = 1;
for steps = 1:1000
w = 2*pi*freq;
r = 2*damping.*sqrt(k*m);
Y = k-m*w.^2+1i*w*r;
% finite difference
K = zeros(N,N); F = zeros(N,1); dx = L/(N-1);
for ii = 2:N-1
K(ii,ii-1) = -1;
K(ii,ii+1) = -1;
K(ii,ii) = 2-dx*dx*w*w*(2*rho*b(ii)/S0(ii)/Y(ii)+1/c^2 );
end
K(1,1) = 1; F(1) = P0;
K(N,N) = 1; F(N) = 0;
P = K\F;
y = -2*P./Y;
% rho*du/dt = -dp/dx ==> -rho w^2 Us = [ p(1)-p(2) ] / dx
Us = ( P(1)-P(2) )/dx/(-rho*w^2);
y0 = 1i*y*w;
y = y./Us;
% revise damping
damping1 = 0.01+0.29./(1+exp( -2*(log10(abs(y0))+4)) );
error = max(abs((damping1-damping)./damping1));
if error<0.01
break;
end
damping = damping1;
end
figure(1);
subplot(2,2,1); hold on; grid on;
plot(x, 28*log10(abs(P)), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('pressure difference in dB');
set(gca,'ylim',[-150,50]);
subplot(2,2,2); hold on; grid on;
plot(x, real(y), 'r-', 'linewidth', 2);
plot(x, abs(y), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('BM displacement re stapes');
subplot(2,2,3); hold on; grid on;
plot(x, 20*log10( abs(y) ), 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('BM displacement amp. in dB');
set(gca,'ylim',[-30,40]);
subplot(2,2,4); hold on; grid on;
plot(x, damping, 'k-', 'linewidth', 2);
xlabel('distance from the stapes, x (m)');
ylabel('damping coefficients');
fprintf(1,'frequency: %6d Hz, maximum BM disp. %e, damping error %f \n', freq, max(abs(y0)),error );
end
%plot inline --size 1200,600
cochlea_model_1d_nonlinear_damping_velocity(1000,10);
cochlea_model_1d_nonlinear_damping_velocity(1000,1);
cochlea_model_1d_nonlinear_damping_velocity(1000,0.1);
cochlea_model_1d_nonlinear_damping_velocity(1000,0.01);
cochlea_model_1d_nonlinear_damping_velocity(5000,10);
cochlea_model_1d_nonlinear_damping_velocity(5000,1);
cochlea_model_1d_nonlinear_damping_velocity(5000,0.1);
cochlea_model_1d_nonlinear_damping_velocity(5000,0.01);
Active 1D Models¶
- The cochlea produces energy
- Negetive damping models was early used for mimicking the active cochlea
- By applying force we create nonlinear feedback models
- Force and negetive damping are synonymous
Zwicker E. A model describing nonlinearities in hearing by active processes with saturation at 40 dB[J]. Biological cybernetics, 1979, 35(4): 243-250.
Furst M, Lapid M. A cochlear model for acoustic emissions[J]. The Journal of the Acoustical Society of America, 1988, 84(1): 222-229.
Time-domain solutions - passive¶
Here we discuss the time-domain solution of 1D cochlear model, controled by $$ \boxed{ \frac{1}{c^2}\frac{\partial^2p_-}{\partial t^2} - \frac{\partial^2 p_-}{\partial x^2} = \frac{\rho b\ddot{\eta}}{S_0} }$$ $$ \boxed{ k(x,t)\eta(x,t)+r(x,t)\dot{\eta}(x,t)+m(x,t)\ddot{\eta}(x,t) = −2p_- }$$
We have
$$ \left[ \begin{array}{cc} M_{PP} & M_{P\eta} \\ 0 & M_{\eta\eta} \end{array}\right] \cdot \left\{ \begin{array}{c} \ddot{P} \\ \ddot{\eta} \end{array} \right\} + \left[ \begin{array}{cc} 0 & 0 \\ 0 & R_{\eta\eta} \end{array}\right] \cdot \left\{ \begin{array}{c} \dot{P} \\ \dot{\eta}\end{array} \right\} + \left[ \begin{array}{cc} K_{PP} & 0 \\ K_{\eta P} & K_{\eta\eta} \end{array}\right] \cdot \left\{ \begin{array}{c} P \\ \eta \end{array} \right\} = \left\{ \begin{array}{c} F_P \\ F_\eta \end{array} \right\} $$where $$ \begin{align} & M_{PP} = \frac{1}{c^2} {I}, \qquad M_{P\eta} = \frac{-\rho b(x)}{S_0(x)} {I}, \qquad {M}_{\eta\eta} = m(x) {I}, \qquad {R}_{\eta\eta} = r(x) {I} \\ & {K}_{PP}\textrm{(i,i-1:i+1)} = -\frac{[1, -2, 1]}{\Delta x^2}, \qquad {K}_{\eta P} = +2 {I}, \qquad {K}_{\eta\eta} = k(x) {I} \end{align} $$
Composite method¶
We consider a dynamic system $M\ddot{x}+R\dot{x}+Kx=f$, we may use the two-step composite method (Bathe, in ADINA).
- First step $t\rightarrow t+\gamma\Delta t$:
- $ x^{t+\gamma\Delta t} = x^t+\gamma\Delta t\dot{x}^{t+\frac{1}{2}\gamma\Delta t}=x^t+\frac{\gamma\Delta t}{2}\left( \dot{x}^t+\dot{x}^{t+\gamma\Delta t}\right)$
- $ \dot{x}^{t+\gamma\Delta t} = \dot{x}^t+\gamma \Delta t\ddot{x}^{t+\frac{1}{2}\gamma\Delta t}=\dot{x}^t+\frac{\gamma\Delta t}{2}\left( \ddot{x}^t+\ddot{x}^{t+\gamma\Delta t}\right)$
- thus $ \dot{x}^{t+\gamma\Delta t} = \frac{2}{\gamma\Delta t} \left( x^{t+\gamma\Delta t}-x^t \right) -\dot{x}^t$
- thus $ \ddot{x}^{t+\gamma\Delta t} = \frac{2}{\gamma\Delta t} \left( \dot{x}^{t+\gamma\Delta t}-\dot{x}^t \right) -\ddot{x}^t = \frac{2}{\gamma\Delta t} \left( \frac{2}{\gamma\Delta t} \left( x^{t+\gamma\Delta t}-x^t \right) -\dot{x}^t -\dot{x}^t \right) -\ddot{x}^t = \frac{4}{\gamma^2\Delta t^2}\left( x^{t+\gamma\Delta t}-x^t \right)-\frac{4}{\gamma\Delta t}\dot{x}^t-\ddot{x}^t $
- substitute them into the equation $M\ddot{x}^{t+\gamma\Delta t}+R\dot{x}^{t+\gamma\Delta t}+Kx^{t+\gamma\Delta t}=f^{t+\gamma\Delta t}$
- $\left( \frac{4}{\gamma^2\Delta t^2} M + \frac{2}{\gamma\Delta t}R + K \right)x^{t+\gamma\Delta t} =\frac{4}{\gamma\Delta t}M\dot{x}^t+M\ddot{x}^t +\frac{2}{\gamma\Delta t}Rx^t+R\dot{x}^t+f^{t+\gamma\Delta t} $
- Second step $t+\gamma\Delta t\rightarrow t+\Delta t$:
- Using 2-order Taylor analysis we have $\dot{x}^{t+\Delta t}=c_1x^t+c_2x^{t+\gamma\Delta t}+c_3x^{t+\Delta t}$
- Similarly, $\ddot{x}^{t+\Delta t}=c_1\dot{x}^t+c_2\dot{x}^{t+\gamma\Delta t}+c_3\dot{x}^{t+\Delta t}$
- $c_1=\frac{1-\gamma}{\gamma\Delta t}, \qquad c_2=-\frac{1}{(1-\gamma)\gamma\Delta t}, \qquad c_3=\frac{2-\gamma}{(1-\gamma)\Delta t}$
- Consider $M\ddot{x}^{t+\Delta t}+R\dot{x}^{t+\Delta t}+Kx^{t+\Delta t}=f^{t+\Delta t}$, we have
- $(c_3^2M+c_3R+K)x^{t+\Delta t} = f^{t+\Delta t}-(c_1c_3M+c_1R)x^t-(c_2c_3M+c_2R)x^{t+\gamma\Delta t}-c_1M\dot{x}^t-c_2M\dot{x}^{t+\gamma\Delta t}$
For minimal error, $\gamma = 1/\sqrt{2}$.
%%file cochlea_model_1d_passive_time.m
function cochlea_model_1d_passive_time(t,p0,plotstyle)
N = 401; L=0.035;
x = linspace(0,L,N)';
S0 = 1e-4*(0.029-0.5*x);
b = 1e-2*(0.019+0.93*x);
k = 1.72e10*exp(-200*x);
m = 1.43;
damping = 0.05*ones(N,1);
r = 2*damping.*sqrt(k*m);
c = 1430;
rho = 1000;
dx = L/(N-1);
[M,R,K] = generateMatrix(N,S0,b,k,m,r,rho,c,dx);
X0 = zeros(2*N,1);
dX0 = zeros(2*N,1);
ddX0 = zeros(2*N,1);
figure(1); hold on; grid on;
line = plot(x,X0(N+1:end),'k-','linewidth',2);
up = 0*x; dn = 0*x;
upline = plot(x,up,'r.');
dnline = plot(x,dn,'r.');
xlabel('distance from the stapes, x (m)');
ylabel('BM displacement, (m)');
for kk = 2:length(t)
% time development
[X2,dX2,ddX2] = compositeMethod(X0,dX0,ddX0,M,R,K,t(kk-1:kk),p0(kk-1:kk));
X0 = X2; dX0 = dX2; ddX0 = ddX2;
y = X0(N+1:end);
up = up*0.996;
dn = dn*0.996;
up = max([up y]')';
dn = min([dn y]')';
if plotstyle==1
if kk<length(t)
continue;
end
end
set(line,'yData',y);
set(upline,'yData',up);
set(dnline,'yData',dn);
title(sprintf('time: %10.6f',t(kk)));
axis([0,0.035,-3e-8,3e-8]);
drawnow(); pause(0.02);
end
end
% generate stiff matrices
function [M,R,K] = generateMatrix(N,S0,b,k,m,r,rho,c,dx)
M0 = sparse(N,N);
Mpp = sparse(2:N-1,2:N-1,1/c^2*ones(N-2,1),N,N);
Mpu = sparse(2:N-1,2:N-1,-rho*b(2:N-1)./S0(2:N-1),N,N);
Muu = sparse(1:N,1:N,m*ones(N,1),N,N);
Mup = M0;
Ruu = sparse(1:N,1:N,r,N,N);
Rpp = M0;
Rpu = M0;
Rup = M0;
Kuu = sparse(1:N,1:N,k,N,N);
Kup = sparse(1:N,1:N,2*ones(N,1),N,N);
Kpu = M0;
idx = zeros(3*N,1); jdx = idx; tmp = idx; flag=0;
for ii = 2:N-1
idx(flag+1:flag+3) = [ii ii ii];
jdx(flag+1:flag+3) = [ii-1,ii,ii+1];
tmp(flag+1:flag+3) = -[1,-2,1]/dx/dx;
flag = flag + 3;
end
Kpp = sparse(idx(1:flag),jdx(1:flag),tmp(1:flag),N,N);
M = [Mpp,Mpu;Mup,Muu];
R = [Rpp,Rpu;Rup,Ruu];
K = [Kpp,Kpu;Kup,Kuu];
end
% time development
function [X2,dX2,ddX2] = compositeMethod(X0,dX0,ddX0,M,R,K,t,p)
N = size(M,1)/2;
gamma = 1/sqrt(2);
dt = t(2)-t(1);
p0 = p(1); p2 = p(1); p1 = p0+gamma*(p2-p0);
% first step
KK = 4/gamma^2/dt/dt*M+2/gamma/dt*R+K;
FF = 4/gamma^2/dt/dt*M*X0+4/gamma/dt*M*dX0+M*ddX0+2/gamma/dt*R*X0+R*dX0;
tmp = max(abs(diag(KK)));
KK(1,1) = tmp; FF(1) = p1*tmp;
KK(N,N) = tmp; FF(N) = 0;
X1 = KK\FF;
dX1 = 2/gamma/dt*(X1-X0)-dX0;
ddX1 = 2/gamma/dt*(dX1-dX0)-ddX0;
% second step
c1 = (1-gamma)/gamma/dt;
c2 = -1/gamma/dt/(1-gamma);
c3 = (2-gamma)/(1-gamma)/dt;
KK = c3^2*M+c3*R+K;
FF = -(c1*c3*M+c1*R)*X0-(c2*c3*M+c2*R)*X1-c1*M*dX0-c2*M*dX1;
tmp = max(abs(diag(KK)));
KK(1,1) = tmp; FF(1) = p2*tmp;
KK(N,N) = tmp; FF(N) = 0;
X2 = KK\FF;
dX2 = c1*X0+c2*X1+c3*X2;
ddX2 = c1*dX0+c2*dX1+c3*dX2;
end
%plot native
% run this code to view the real-time animation of the BM vibration
close all; clear all; clc;
f = 1000; dt = 1/f/20;
t = 0:dt:20/f;
p0 = sin(2*pi*f*t);
cochlea_model_1d_passive_time(t,p0,0);
%plot inline --size 1200,400
close all; clear all; clc;
f = 8000; dt = 1/f/20;
t = 0:dt:300/f;
p0 = 8*sin(2*pi*f*t)+4*sin(2*pi*f/2*t)+2*sin(2*pi*f/4*t)+sin(2*pi*f/8*t);
cochlea_model_1d_passive_time(t,p0,1);
As shown above, if the model is passive, different frequency components are resolved at different locations. No distortion were seen.