2D Cochlear Models¶

by Liu-Jie Ren

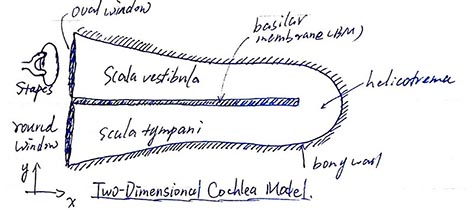
cochlear_model_2d

Notations

Coordinates $x$ and $y$
Field variables
- $p(x,y,t)$ - Pressure of the fluid
- $\vec{v}(x,y,t)$ - Fluid velocity (vector in $x, y$ direction)
Parameters
- $\rho$ - fluid density
- $\mu$ - fluid viscosity
- $c$ - sound speed in fluid
Basilar membrane
- $\eta(x,t)$ - BM displacement
- $k(x)$ - BM stiffness
- $r(x)$ - BM damping
- $m(x)$ - BM mass
subscriptions: we use the subscript $v$ for scala vestibula, $t$ for scala tympani.

Control Equations for Fluid in General¶

Firstly we assume the cochlear fluid is a water-like Newtonian fluid controled by the Navier-Stokes equations. The fluid is assumed to be compressible for now.

The NS equations for compressible fluid are $$\begin{align} & \mathrm{Continuty:\quad} \frac{\partial\rho}{\partial t}+\nabla\left(\rho\vec{v}\right)=0 \\ & \mathrm{Momentum: \quad} \rho\left(\frac{\partial\vec{v}}{\partial t}+\vec{v}\cdot\nabla\vec{v}\right) =-\nabla p+\mu\nabla^2\vec{v}+\frac{1}{3}\mu\nabla(\nabla\cdot\vec{v})+\rho\vec{g} \end{align}$$

Simplifications

We assume no body force so that $\vec{g}=0$,
No convective term so that $\vec{v}\cdot\nabla\vec{v}=0$,thus the momentum equation becomes $\displaystyle \rho\frac{\partial\vec{v}}{\partial t} =-\nabla p+\mu\nabla^2\vec{v}+\frac{1}{3}\mu\nabla(\nabla\cdot\vec{v})$

For different assumptions, we can make different forms

Acoustic compressible and viscous For acoutic flow, we assume $\rho$ is nearly a constant and $\displaystyle \frac{\partial p}{\partial \rho} = c^2$, $\displaystyle\frac{\partial\rho}{\partial t}=\frac{1}{c^2}\frac{\partial p}{\partial t}$, $$\begin{align} &\frac{1}{c^2}\frac{\partial p}{\partial t}+\nabla\left(\rho\vec{v}\right)=0 \rightarrow \frac{1}{c^2}\frac{\partial p}{\partial t}+\rho\nabla\vec{v}=0\\ &\rho\frac{\partial\vec{v}}{\partial t}=-\nabla p+\mu\nabla^2\vec{v}+\frac{1}{3}\mu\nabla(\nabla\cdot\vec{v}) \end{align}$$ by assuming $$\vec{v}\cdot\nabla\rho\approx 0$$

Incompressible and viscous

If the fluid is incompressible, then $\partial\rho/\partial t=0$ and $\nabla\vec{v}=0$, thus $$ \begin{align} &\nabla\vec{v} = 0 \\ &\rho\frac{\partial\vec{v}}{\partial t}=-\nabla p+\mu\nabla^2\vec{v} \end{align}$$

Acoustic compressible and invicid

If the fluid in invicid, then $\nu=0$, thus $$ \begin{align} &\frac{1}{c^2}\frac{\partial p}{\partial t}+\nabla\left(\rho\vec{v}\right)=0 \rightarrow \frac{1}{c^2}\frac{\partial p}{\partial t}+\rho\nabla\vec{v}=0 \rightarrow \frac{1}{c^2}\frac{\partial^2p}{\partial t^2}+\rho\frac{\partial \nabla\vec{v}}{\partial t}=0 \\ &\rho\frac{\partial\vec{v}}{\partial t}=-\nabla p \rightarrow \rho\nabla\left(\frac{\partial\vec{v}}{\partial t}\right)=-\nabla^2 p \end{align}$$

Thus $$ \frac{1}{c^2}\frac{\partial p}{\partial t}-\nabla^2 p = 0$$

Incompressible and invicid $$ \begin{align} &\nabla\cdot\vec{v} = 0 \\ &\rho\frac{\partial\vec{v}}{\partial t}=-\nabla p \end{align}$$ Thus $$\nabla^2 p = 0$$

For the fluid field, if we use the viscous assumption, we should solve the pressure and displacement/velocity field together, as shown in Cheng (2008) and Ren (2018). The mixed finite element method could be a little bit complicated (the researchers have to deal with the stability), we would discuss it later.

However, if we use the invicid assumption, whether compressible or incompressible (as most models used), we can solve the fluid pressure field only. For incompressilbe flow, $$\nabla^2 p = 0$$ and for compressilbe acoutic flow, $$\frac{1}{c^2}\frac{\partial p}{\partial t} - \nabla^2 p = 0$$

Boundary conditions For the fluid pressure field, we have 2 types of boundary conditions.

Dirichlet B.C.
- the fluid pressure should be a given, $p = \bar{p}$
Neumann B.C.
- the normal fluid displacement/velocity is given, since $\rho\partial\vec{v_n}/\partial t=\rho \vec{a}_n=-\nabla p\cdot\vec{n}$
- $\nabla p \cdot \vec{n} = 0$ for wall
- $\nabla p \cdot \vec{n} = -\rho a_n $ for given normal accelaration

Coupling with the BM

Two conditions should be satisfied

Displacement/velocity
- thus $\nabla p\cdot\vec{n}=\rho a_n$ where $a_n$ is decided by the BM movement
Force
- $ m\ddot{\eta}+r\dot{\eta}+k\eta = f(p)$ the movement of BM is driven by the fluid force

Symmetrical box model (2D)¶

Early 2d cochlear models made geometrical simplication for the cochlea. Here we start with Neely(1981)'s model.

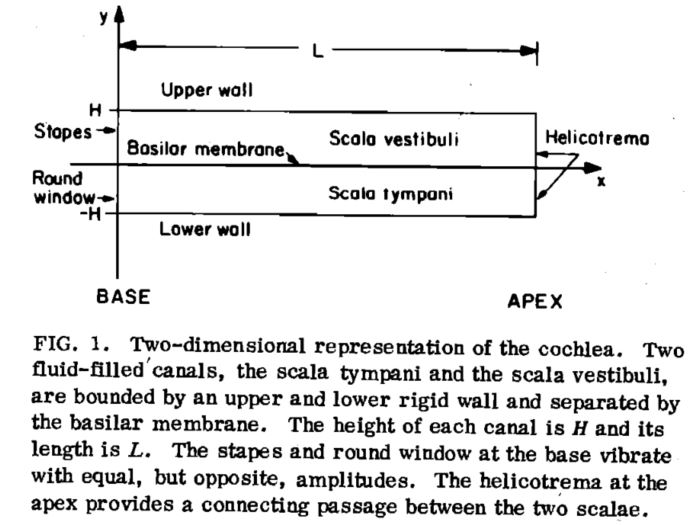
2d_cochlea_model_neely

Control equations¶

In Neely's model, the fluid is assumed to be incompressible and invicid, thus $$\nabla\cdot\vec{v}_v=0,\qquad \rho\frac{\partial\vec{v}_v}{\partial t}=-\nabla p_v\qquad x\in[0,L],y\in[0,H]$$ $$\nabla\cdot\vec{v}_t=0,\qquad \rho\frac{\partial\vec{v}_t}{\partial t}=-\nabla p_t\qquad x\in[0,L],y\in[0,-H]$$ Assume that $\vec{v}(x,y)=\vec{v}_v(x,y)-\vec{v}_t(x,-y)$ and $p(x,y)=p_v(x,y)-p_t(x,-y)$

Governing equations

For compressible flow: $\frac{1}{c^2}\frac{\partial p}{\partial t}-\nabla^2p=0$; for incompressible flow: $\nabla^2p=0$.

Boundary conditions

At the upper wall, $\vec{v}_v\cdot\vec{n}=0$; at the lower wall $\vec{v}_t\cdot\vec{n}=0$, thus $\vec{v}\cdot\vec{n}=0$, and $\boxed{\nabla p\cdot\vec{n}=0}$ or simply $\boxed{\partial p/\partial y=0}$
At the base, $\nabla p_v\cdot\vec{n}=-\rho\dot{v}_v\cdot\vec{n} = \rho \ddot{u}_{st}$, $\nabla p_t\cdot\vec{n}=-\rho\dot{v}_t\cdot\vec{n} = \rho \ddot{u}_{rw}$, thus $\boxed{ \nabla p\cdot\vec{n}=2\rho\ddot{u}_{st}}$ or $\boxed{ \partial p/\partial x=-2\rho\ddot{u}_{st}}$
For the BM, we have $\nabla p_v\cdot\vec{n}=-\rho\dot{v}_v\cdot\vec{n}= \rho\ddot{\eta}$ and $\nabla p_t\cdot\vec{n}=-\rho\ddot{\eta}$, thus $\boxed{ \nabla p\cdot\vec{n} = 2\rho\ddot{\eta} }$ or $\boxed{\partial p/\partial y=-2\rho\ddot{\eta}}$

Basilar Membrane $m(x)\ddot{\eta}(x)+r(x)\cdot{\eta}(x)+k(x)\eta(x) = p_t(x,y=0)-p_v(x,y=0)=-p(x)$

Frequency domain solution¶

Assume that $p(x,y,t) = P(x,y)\exp(j\omega t)$, then

Control Equation $$ -\frac{j\omega}{c^2}P+\nabla^2 P = 0 \quad \mathrm{for~compressible~flow} \\ \nabla^2 P = 0 \quad \mathrm{for~incompressible~flow} $$ Boundary Domain

For the upper wall, $\frac{\partial P}{\partial y}=0$
For the left wall, $\frac{\partial P}{\partial x} = 2\rho\omega^2 U_{st}$
For the right wall, $P = 0$
For the bottom wall (BM), $\frac{\partial P}{\partial y}=2\rho\omega^2\eta$
and $-P=Z(x)\eta$, thus $\frac{\partial P}{\partial y}=\frac{-2\rho\omega^2}{Z(x)}P$

Finite Difference Method The solutions were given using Neely's finite difference method (1981).

Neely S T. Finite difference solution of a two‐dimensional mathematical model of the cochlea[J]. The Journal of the Acoustical Society of America, 1981, 69(5): 1386-1393.

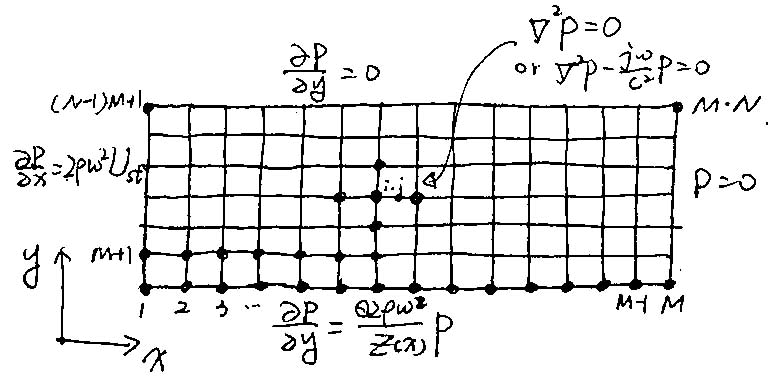
cochlea_model_2d_finite_difference

We divide the fluid domain into $M\times N$ grids. Each grid is represented by a unique pair $(i,j)$, or a unique number $(N-1)\times j+i$

%%file cochlea_model_2d_passive_neely.m
function [P,nod,ele]=cochlea_model_2d_passive_neely(freq,Us)
    M = 257; N = 17;
    L = 0.035; H = 0.001;
    rho = 1000; c = 1430;
    x = linspace(0,L,M)';
    m = 1.5;
    r = 2000;
    k = 1e10*exp(-200*x);
    grids = reshape(1:M*N,M,N);
    dx = L/(M-1); dxx = 1/(dx*dx);
    dy = H/(N-1); dyy = 1/(dy*dy);
    
    w = 2*pi*freq;
    Z = k-m*w*w+1i*w*r;
    idx = zeros(5*M*N,1);
    jdx = zeros(5*M*N,1);
    tmp = zeros(5*M*N,1);
    flag = 0;

    FF = zeros(M*N,1);
    % the domain | Pxx+Pyy-jw/c/c*P=0
    for ii = 2:M-1
        for jj = 2:N-1
            pc = grids(ii,jj);
            pn = grids(ii,jj+1);
            ps = grids(ii,jj-1);
            pw = grids(ii-1,jj);
            pe = grids(ii+1,jj);
            idx(flag+1:flag+5) = [pc pc pc pc pc];
            jdx(flag+1:flag+5) = [pn ps pw pe pc];
            % tmp(flag+1:flag+5) = [dyy,dyy,dxx,dxx,-2*dxx-2*dyy-1i*w/c/c]; %compressible
            tmp(flag+1:flag+5) = [dyy,dyy,dxx,dxx,-2*dxx-2*dyy]; %incompressible
            flag = flag+5;
        end
    end
    % upper | Py=0
    for ii = 1:M
        pc = grids(ii,N);
        ps = grids(ii,N-1);
        idx(flag+1:flag+2) = [pc,pc];
        jdx(flag+1:flag+2) = [pc,ps];
        tmp(flag+1:flag+2) = [1,-1]/dy;
        flag = flag + 2;
    end
    % bottom | Py + 2\rho*w*w/Z * P = 0
    for ii = 1:M
        pc = grids(ii,1);
        pn = grids(ii,2);
        idx(flag+1:flag+2) = [pc,pc];
        jdx(flag+1:flag+2) = [pc,pn];
        tmp(flag+1:flag+2) = [-1/dy+2*rho*w*w/Z(ii),1/dy];
        flag = flag + 2;
    end
    % left | Px = 2 \rho w*w Us
    for jj = 2:N-1
        pc = grids(1,jj);
        pe = grids(2,jj);
        idx(flag+1:flag+2) = [pc,pc];
        jdx(flag+1:flag+2) = [pc,pe];
        tmp(flag+1:flag+2) = [-1,1]/dx;
        FF(pc) = 2*rho*w*w*Us;
        flag = flag + 2;
    end
    % right| P = 0
    for jj = 2:N-1
        pc = grids(M,jj);
        idx(flag+1) = [pc];
        jdx(flag+1) = [pc];
        tmp(flag+1) = [1]/dx;
        FF(pc) = 0;
        flag = flag + 1;
    end
    KK = sparse(idx(1:flag),jdx(1:flag),tmp(1:flag),M*N,M*N);
    P = KK\FF;
    [nod,ele] = createGridMesh(M,N,L,H);
    pressure = P(grids(1:M,1));
    displacement = -pressure./Z;
        
    figure(1);
    subplot(2,2,1); hold on; grid on;
    plot(x, 20*log10(abs(pressure)), 'k-', 'linewidth', 2);
    xlabel('distance from the stapes, x (m)');
    ylabel('pressure difference in dB'); 
    set(gca,'xlim',[0,L],'ylim',[70,200]);
    
    subplot(2,2,2); hold on; grid on;
    plot(x, 20*log10(abs(displacement/Us)), 'k-', 'linewidth', 2);
    xlabel('distance from the stapes, x (m)');
    ylabel('BM displacement re stapes in dB');
    set(gca,'xlim',[0,L],'ylim',[-45,20]);
    
    subplot(2,2,3); hold on; grid on;
    plot(x, unwrap(angle(pressure))/pi, 'k-', 'linewidth', 2);
    xlabel('distance from the stapes, x (m)');
    ylabel('pressure phase, \pi');
    set(gca,'xlim',[0,L]);
    
    subplot(2,2,4); hold on; grid on;
    plot(x, unwrap(angle(displacement))/pi, 'k-', 'linewidth', 2);
    xlabel('distance from the stapes, x (m)');
    ylabel('disp. phase, \pi');
    set(gca,'xlim',[0,L]);
end

function [nod,ele] = createGridMesh(M,N,L,H)
    dx = L/(M-1);
    dy = H/(N-1);
    nod = zeros(M*N,2);
    kk = 1;
    for jj = 1:N
        for ii = 1:M
            nod(kk,:) = [dx*(ii-1) dy*(jj-1)];
            kk = kk + 1;
        end
    end
    ele = zeros((M-1)*(N-1),4);
    kk = 1;
    for jj = 1:N-1
        for ii = 1:M-1
            n1 = M*(jj-1)+ii;
            n2 = n1+1;
            n3 = n2+M;
            n4 = n3-1;
            ele(kk,:) = [n1,n2,n3,n4];
            kk = kk + 1;
        end
    end
end

Created file 'C:\Users\RenLi\__model_cochlea\cochlea_model_2d_passive_neely.m'.

%plot inline --size 800,400
cochlea_model_2d_passive_neely(500,1);
[P,nod,ele]=cochlea_model_2d_passive_neely(1000,1);
cochlea_model_2d_passive_neely(2000,1);
cochlea_model_2d_passive_neely(4000,1);

%plot inline --size 1000,100
figure(1); patch('Faces',ele,'Vertices',nod,'FaceVertexCData',real(P),'FaceColor','interp','edgecolor','none'); 
title('real(P),1kHz'); colormap('hsv')
figure(2); patch('Faces',ele,'Vertices',nod,'FaceVertexCData',abs(P),'FaceColor','interp','edgecolor','none'); 
title('abs(P),1kHz'); colormap('hsv')

Time-Domain Solution¶

Governing equations

For compressible flow: $-\frac{1}{c^2}\frac{\partial p}{\partial t}+\nabla^2p=0$; for incompressible flow: $\nabla^2p=0$.

Boundary conditions

At the upper wall, $\boxed{\partial p/\partial y=0}$
For the BM, $\boxed{\partial p/\partial y=-2\rho\ddot{\eta}}$
At the base, $\boxed{ \partial p/\partial x=-2\rho\ddot{u}_{st}}$
At right, $\boxed{p=0}$

Basilar Membrane $m(x)\ddot{\eta}(x)+r(x)\cdot{\eta}(x)+k(x)\eta(x) =-p(x)$

$$ \left[ \begin{array}{cc} M_{pp} & M_{p\eta} \\ M_{\eta p} & M_{\eta\eta}\end{array}\right] \cdot\left\{\begin{array}{c} \ddot{P} \\ \ddot{\eta} \end{array}\right\} + \left[ \begin{array}{cc} R_{pp} & R_{p\eta} \\ R_{\eta p} & R_{\eta\eta}\end{array}\right] \cdot\left\{\begin{array}{c} \dot{P} \\ \dot{\eta} \end{array}\right\} + \left[ \begin{array}{cc} K_{pp} & K_{p\eta} \\ K_{\eta p} & K_{\eta\eta}\end{array}\right] \cdot\left\{\begin{array}{c} {P} \\ {\eta} \end{array}\right\} =\left\{\begin{array}{c} F_{P} \\ F_{\eta} \end{array}\right\}$$

Here $$M_{pp}=0, \quad M_{p\eta}=0, \quad M_{\eta p}=0, \quad M_{\eta\eta}=mI \\ R_{pp}=0 \mathrm{~incompressible}, R_{pp}=-\frac{1}{c^2}I \mathrm{~compressible}, \quad R_{p\eta}=0,\quad R_{\eta p}=0,\quad R_{\eta\eta} = rI \\ K_{pp}=\mathrm{Lapalce~term}, \quad K_{p\eta}=0, \quad K_{\eta p}=1\textrm{~for~some~points},\quad K_{\eta\eta}=kI $$ and the boundary conditions should be implemented.

$$ \left[ \begin{array}{cc} 0 & M^*_{p\eta} \\ 0 & M_{\eta\eta}\end{array}\right] \cdot\left\{\begin{array}{c} \ddot{P} \\ \ddot{\eta} \end{array}\right\} + \left[ \begin{array}{cc} R_{pp} & 0 \\ 0 & R_{\eta\eta}\end{array}\right] \cdot\left\{\begin{array}{c} \dot{P} \\ \dot{\eta} \end{array}\right\} + \left[ \begin{array}{cc} K_{pp} & 0 \\ K_{\eta p} & K_{\eta\eta}\end{array}\right] \cdot\left\{\begin{array}{c} {P} \\ {\eta} \end{array}\right\} =\left\{\begin{array}{c} F_{P} \\ F_{\eta} \end{array}\right\}$$

where $M^*_{p\eta}$ is from the boundary condition $\partial p/\partial y=-2\rho\ddot{\eta}$.

%%file cochlea_model_2d_passive_neely_time.m
function cochlea_model_2d_passive_neely_time(t,Ast,plotstyle)
    M = 257; N = 17;
    L = 0.035; H = 0.001;
    rho = 1000; c = 1430;
    x = linspace(0,L,M)';
    m = 1.5;
    r = 2000;
    k = 1e10*exp(-200*x);
    grids = reshape(1:M*N,M,N);
    dx = L/(M-1); dxx = 1/(dx*dx);
    dy = H/(N-1); dyy = 1/(dy*dy);
    [nod,ele] = createGridMesh(M,N,L,H);
    % m \ddot{\eta} + r\dot{\eta} + k\eta + 2p = 0
    Fp  = zeros(M*N,1);
    Fe  = zeros(M,1);
    Mee = sparse(1:M,1:M,m.*ones(M,1),M,M);
    Mep = sparse(M,M*N);
    Ree = sparse(1:M,1:M,r.*ones(M,1),M,M);
    Rep = sparse(M,M*N);
    Kee = sparse(1:M,1:M,k.*ones(M,1),M,M);
    Kep = sparse(1:M,1:M,2.*ones(M,1),M,M*N);
    Mpp = sparse(M*N,M*N);
    Rpe = sparse(M*N,M);
    Kpe = sparse(M*N,M);
    % \nabla^2 p - 1/c/c*\dot{p} = 0 ==> Kpp and Rpp for inner nodes
    Kppidx = zeros(5*M*N,1); Kppjdx = Kppidx; Kpptmp = Kppidx; Kppflag = 0;
    Rppidx = zeros(5*M*N,1); Rppjdx = Rppidx; Rpptmp = Rppidx; Rppflag = 0;
    for ii = 2:M-1
        for jj = 2:N-1
            pc = grids(ii,jj); pn = grids(ii,jj+1); ps = grids(ii,jj-1);
            pw = grids(ii-1,jj); pe = grids(ii+1,jj);
            Kpplist = Kppflag+1:Kppflag+5;
            Kppidx(Kpplist) = [pc pc pc pc pc];
            Kppjdx(Kpplist) = [pn ps pw pe pc];
            Kpptmp(Kpplist) = [dyy dyy dxx dxx -2*dxx-2*dyy];
            Kppflag = Kppflag + 5;
            Rpplist = Rppflag+1;
            Rppidx(Rpplist) = [pc];
            Rppjdx(Rpplist) = [pc];
            Rpptmp(Rpplist) = -1/c/c;
        end
    end
    % Upper nodes dp/dy = 0 ===> only affects Kpp
    for ii = 1:M
        pc = grids(ii,N); ps = grids(ii,N-1);
        Kpplist = Kppflag+1:Kppflag+2;
        Kppidx(Kpplist) = [pc pc];
        Kppjdx(Kpplist) = [pc ps];
        Kpptmp(Kpplist) = [-1  1]/dy;
        Kppflag = Kppflag + 2;
    end
    % Bottom nodes dp/dy + 2\rho\ddot{\eta} = 0  ===> Kpp and Mpe
    for ii = 1:M
        pc = grids(ii,1); pn = grids(ii,2);
        Kpplist = Kppflag+1:Kppflag+2;
        Kppidx(Kpplist) = [pc pc];
        Kppjdx(Kpplist) = [pc pn];
        Kpptmp(Kpplist) = [-1  1]/dy;
        Kppflag = Kppflag + 2;
    end
    Mpe = sparse(1:M,1:M,2*rho*ones(M,1),M*N,M);
    % Left nodes dp/dx = -2 \rho Ast ==> Kpp and Fp 
    for jj = 2:N-1
        pc = grids(1,jj); pe = grids(2,jj);
        Kpplist = Kppflag+1:Kppflag+2;
        Kppidx(Kpplist) = [pc pc];
        Kppjdx(Kpplist) = [pc pe];
        Kpptmp(Kpplist) = [-1  1]/dx/(-2)/rho;
        Kppflag = Kppflag + 2; 
    end
    % Fp should generate for each time step
    % Right nodes p = 0 ====> Kpp and Fp
    for jj = 2:N-1
        pc = grids(M,jj);
        Kpplist = Kppflag+1;
        Kppidx(Kpplist) = [pc];
        Kppjdx(Kpplist) = [pc];
        Kpptmp(Kpplist) = 1/dx/dy;
        Kppflag = Kppflag + 1;
        Fp(pc) = 0;
    end
    Kpp = sparse(Kppidx(1:Kppflag),Kppjdx(1:Kppflag),Kpptmp(1:Kppflag),M*N,M*N);
    Rpp = sparse(Rppidx(1:Rppflag),Rppjdx(1:Rppflag),Rpptmp(1:Rppflag),M*N,M*N);
    MMMM = [Mpp Mpe; Mep Mee];
    RRRR = [Rpp Rpe; Rep Ree];
    KKKK = [Kpp Kpe; Kep Kee];
    FFFF = [Fp; Fe];
    X0 = zeros(M*N+M,1);
    dX0 = zeros(M*N+M,1);
    ddX0 = zeros(M*N+M,1);
    
    figure(1); hold on; grid on;
    line = plot(x,X0(end-M+1:end),'k-','linewidth',2);
    up = 0*x; dn = 0*x;
    upline = plot(x,up,'r.');
    dnline = plot(x,dn,'r.');
    xlabel('distance from the stapes, x (m)');
    ylabel('BM displacement, (m)');
    
    for kk = 2:length(t)
        % time development
       [X2,dX2,ddX2] = compositeMethod(X0,dX0,ddX0,MMMM,RRRR,KKKK,FFFF,t(kk-1:kk),Ast(kk-1:kk),grids); 
       X0 = X2; dX0 = dX2; ddX0 = ddX2;
       y  = X0(end-M+1:end);
       up = up*0.996;
       dn = dn*0.996;
       up = max([up y]')';
       dn = min([dn y]')';
       if plotstyle==1
           if kk<length(t)
               continue;
           end
       end
       set(line,'yData',y);
       set(upline,'yData',up);
       set(dnline,'yData',dn);
       title(sprintf('time: %10.6f',t(kk)));
       axis([0,0.035,-10,10]);
       drawnow(); pause(0.02);
    end
end

function [nod,ele] = createGridMesh(M,N,L,H)
    dx = L/(M-1);
    dy = H/(N-1);
    nod = zeros(M*N,2);
    kk = 1;
    for jj = 1:N
        for ii = 1:M
            nod(kk,:) = [dx*(ii-1) dy*(jj-1)];
            kk = kk + 1;
        end
    end
    ele = zeros((M-1)*(N-1),4);
    kk = 1;
    for jj = 1:N-1
        for ii = 1:M-1
            n1 = M*(jj-1)+ii;
            n2 = n1+1;
            n3 = n2+M;
            n4 = n3-1;
            ele(kk,:) = [n1,n2,n3,n4];
            kk = kk + 1;
        end
    end
end

% time development
function [X2,dX2,ddX2] = compositeMethod(X0,dX0,ddX0,M,R,K,F,t,p,grids)
    [m,n] = size(grids);
    gamma = 1/sqrt(2);
    dt = t(2)-t(1);
    p0 = p(1); p2 = p(1); p1 = p0+gamma*(p2-p0); 
    % first step
    points = grids(1,2:n-1);
    Ft = F; Ft(points) = p1;
    KK = 4/gamma^2/dt/dt*M+2/gamma/dt*R+K;
    FF = Ft+4/gamma^2/dt/dt*M*X0+4/gamma/dt*M*dX0+M*ddX0+2/gamma/dt*R*X0+R*dX0;
    X1 = KK\FF;
    dX1 = 2/gamma/dt*(X1-X0)-dX0;
    ddX1 = 2/gamma/dt*(dX1-dX0)-ddX0;
    % second step
    c1 = (1-gamma)/gamma/dt;
    c2 = -1/gamma/dt/(1-gamma);
    c3 = (2-gamma)/(1-gamma)/dt;
    KK = c3^2*M+c3*R+K;
    Ft = F; Ft(points) = p2;
    FF = Ft-(c1*c3*M+c1*R)*X0-(c2*c3*M+c2*R)*X1-c1*M*dX0-c2*M*dX1;
    X2 = KK\FF;
    dX2 = c1*X0+c2*X1+c3*X2;
    ddX2 = c1*dX0+c2*dX1+c3*dX2;
end

Created file 'C:\Users\RenLi\__model_cochlea\cochlea_model_2d_passive_neely_time.m'.

%plot native
% run this code to view the real-time animation of the BM vibration 
close all; clear all; clc;
f = 1000; dt = 1/f/20; w=2*pi*f;
t = [0:dt:20/f]';
Ust = 1;
envelop = 0*t+1;
envelop(1:5/f/dt) = linspace(0,1,5/f/dt);
Ast = -Ust*w*w*sin(w*t).*envelop;
cochlea_model_2d_passive_neely_time(t,Ast,0);

%plot native
close all; clear all; clc;
f = 2000; dt = 1/f/20; w=2*pi*f;
t = [0:dt:40/f]';
Ust = 1;
envelop = 0*t+1;
envelop(1:6/f/dt) = linspace(0,1,6/f/dt);
Ast = (-Ust*w*w*sin(w*t)-Ust*w*w/4*sin(w/2*t)).*envelop;
cochlea_model_2d_passive_neely_time(t,Ast,1);

Two-D Cochlear Model - Finite Element Scheme¶

Previously, we have solved the 2d cochlear model using the finite difference method, here we would develop a finite element scheme. cochlea_model_2d_finite_element

Control equations¶

$$\frac{1}{c^2}\frac{\partial p}{\partial t}-\nabla^2 p=0$$

on Dirichlet boundary: $p=\bar{p}$

on Neumann boundary: $\nabla p\cdot \vec{n}=-\rho \vec{a}\cdot\vec{n}$ where $\vec{a}$ is acceleration.

Frequency domain¶

$$\nabla^2 P - \frac{j\omega}{c^2}P = 0$$

on Dirichlet boundary: $P=\bar{P}$

on Neumann boundary: $\nabla P\cdot\vec{n}=\rho\omega^2 \vec{U}\cdot\vec{n}$ where $\vec{U}$ is the displacement amplitude.

Weak form¶

$$ \int_\Omega \delta P \left( \nabla^2 P -\frac{j\omega}{c^2}P \right) \mathrm{d}\Omega = 0 $$

since $ \int_{\Omega} \delta P \cdot \nabla^{2} P d \Omega=\int_{\Omega} \nabla(\delta P \cdot \nabla P) \mathrm{d} \Omega - \int_{\Omega} \nabla \delta P \cdot \nabla P \mathrm{d} \Omega =\int_{\Gamma_{N}} \delta p \cdot(\nabla P \cdot \vec{n}) \mathrm{d} \Gamma-\int_{\Omega} \nabla \delta P \cdot \nabla P \mathrm{d} \Omega$ the weak form is $$ \int_{\Omega} \nabla \delta P \cdot \nabla P \mathrm{d} \Omega+\frac{j \omega}{c^{2}} \int_{\Omega} \delta P \cdot P \mathrm{d} \Omega=\int_{\Gamma_{N}} \delta P \cdot(\nabla P \cdot \vec{n}) \mathrm{d}\Gamma $$ where $$\int_{\Gamma_{N}} \delta P \cdot(\nabla P \cdot \vec{n}) \mathrm{d}\Gamma = \int_{\Gamma_{N}} \delta P \cdot(-\rho\omega^2 U_n) \mathrm{d}\Gamma$$

Finite element matrices¶

Assume the shape function $N(x,y)=[N_1, N_2, N_3, N_4]$, thus we have

for the term $\int_\Omega \nabla\delta P\cdot \nabla P \mathrm{d}\Omega$: $D_e=N_{x}^T N_x+N_{y}^T N_y$,

for the term $\int_\Omega \nabla\delta P\cdot P\mathrm{d}\Omega$: $M_e = N^{T}N$.

for boundary conditions, at the input (stapes): $\int_{\Gamma_{N}} \delta P \cdot(-\rho\omega^2 U_n) \mathrm{d}\Gamma$: $-\rho\omega^2 U_{stapes}\cdot H^T$

for boundary conditions, on the BM (SV): $\int_{\Gamma_{N}} \delta P \cdot(+\rho\omega^2 U_{BM}) \mathrm{d}\Gamma$ $$ \rho\omega^2 H^T H \left[\begin{array}{c}U_{BM1} \\ U_{BM2}\end{array}\right] = \rho\omega^2 H^T H \left [ \begin{array}{cccc} \frac{1}{Z(x_1)}&-\frac{1}{Z(x_1)}&0&0 \\ 0&0&\frac{1}{Z(x_2)}&-\frac{1}{Z(x_2)}\end{array} \right ] \cdot \left\{ \begin{array}{c} P_{ST1}\\P_{SV1}\\P_{ST2}\\P_{SV2}\end{array}\right\}$$

for boundary conditions, on the BM (ST): $\int_{\Gamma_{N}} \delta P \cdot(-\rho\omega^2 U_{BM}) \mathrm{d}\Gamma$ $$ -\rho\omega^2 H^T H \left[\begin{array}{c}U_{BM1} \\ U_{BM2}\end{array}\right] = -\rho\omega^2 H^T H \left [ \begin{array}{cccc} \frac{1}{Z(x_1)}&-\frac{1}{Z(x_1)}&0&0 \\ 0&0&\frac{1}{Z(x_2)}&-\frac{1}{Z(x_2)}\end{array} \right ] \cdot \left\{ \begin{array}{c} P_{ST1}\\P_{SV1}\\P_{ST2}\\P_{SV2}\end{array}\right\}$$

The program cochlea_model_2d_create_mesh.m create a .mat file to store the mesh information

%%file cochlea_model_2d_create_mesh.m
function cochlea_model_2d_create_mesh(file)
    %% theis function try to create a 2D mesh as ADINA
    L = 0.035; HaSV = 0.001; HbSV = 0.0005; HaST = 0.001; HbST = 0.0005;
    Heli = 0.0005;
    % definition of points
    points.loc=[0,-HaST;        % point 1
                0,-0.00005;            % point 2
                0,0.00005;            % point 3
                0,HaSV;         % point 4
                L,-HbST;        % point 5
                L,0;            % point 6
                L,HbST;         % point 7
                L+Heli,-HbST;   % point 8
                L+Heli, 0;      % point 9
                L+Heli, HbSV];  % point 10
    lines.point=[1,5;  % line 1
                2,6;    % line 2
                3,6;    % line 3
                4,7;    % line 4
                5,8;    % line 5
                6,9;    % line 6
                7,10;   % line 7
                1,2;    % line 8
                5,6;    % line 9
                8,9;    % line 10
                3,4;    % lien 11
                6,7;    % line 12
                9,10];  % line 13
    surfs.line=[1,9,2,8;   % surf 1
                3,12,4,11;  % surf 2
                5,10,6,9;   % surf 3
                6,13,7,12]; % surf 4
    lines.ori = zeros(size(lines.point,1),1);
    surfs.ori = 0*surfs.line;
    points.no= size(points.loc,1);
    lines.no = size(lines.point,1);
    surfs.no = size(surfs.line,1);
    % divisions should be of same length of no. of lines
    lines.division =[256,256,256,256,5,5,5,10,10,10,10,10,10];
    %% analyze the geometry
    % check for line and points
    points.used = zeros(points.no,1);
    for ii = 1:lines.no
        points.used(lines.point(ii,:)) = points.used(lines.point(ii,:))+1;
    end
    if ~isempty(find(points.used<=1))
        fprintf('not all points been used !\n');
    end
    % check for surf and lines
    lines.used = zeros(lines.no,1);
    for ii = 1:surfs.no
        lines.used(surfs.line(ii,:))=lines.used(surfs.line(ii,:))+1;
    end
    if ~isempty(find(lines.used<1))
        fprintf('not all lines been used !\n');
    end
    % check for surf lines orientation
    for kk = 1:surfs.no
        tmp = surfs.line(kk,:);
        pts = lines.point(tmp,:);
        pts = [pts;pts(1,:)];
        for ii = 1:length(tmp)
            n11 = pts(ii,1); n12 = pts(ii,2);
            n21 = pts(ii+1,1); n22 = pts(ii+1,2);
            if n12 == n21 || n12 == n22
                surfs.ori(kk,ii) = 1;
                lines.ori(tmp(ii)) = 1;
            end
            if n11 == n21 || n11 == n22
                surfs.ori(kk,ii) = -1;
                lines.ori(tmp(ii)) = -1;
                pts(ii,1:2) = pts(ii,2:-1:1);
            end
        end
        if ~isempty(find(surfs.ori(kk,:)==0))
            fprintf('problems in surfs orientation\n');
        end
        for ii = 1:length(tmp)-1
            L1 = points.loc(pts(ii,2),:)-points.loc(pts(ii,1),:);
            L2 = points.loc(pts(ii+1,2),:)-points.loc(pts(ii+1,1),:);
            if L1(1)*L2(2)-L1(2)*L2(1)<=0
                fprintf('problems in surfs orientation, negtive\n');
            end
        end
    end
    
    %% Check for mapping
    for kk = 1:surfs.no
        tmp = surfs.line(kk,:);
        if lines.division(tmp(1))~=lines.division(tmp(3)) ...
            || lines.division(tmp(2))~=lines.division(tmp(4))
            fprintf('problems in surfs (surf. %d) mapping \n',kk);
            return;
        end
    end
    
    %% evaluation
    nnod = 0;
    nele = 0;
    for kk = 1:surfs.no
        tmp = surfs.line(kk,:);
        M = lines.division(tmp(1));
        N = lines.division(tmp(2));
        nnod = nnod+(M+1)*(N+1);
        nele = nele+M*N;
    end
    
    %% mesh
    nod = zeros(nnod,2);
    ele = zeros(nele,4);
    % points mesh
    nodkk = 0; elekk = 0;
    nod(nodkk+(1:points.no),:) = points.loc;
    points.nodid = nodkk+(1:points.no);
    nodkk = nodkk + points.no;
    
    % line mesh
    for kk = 1:lines.no
        p1 = lines.point(kk,1);
        p2 = lines.point(kk,2);
        if lines.ori(kk) == -1;
            tmp = p1; p1 = p2; p2 = tmp;
        end
        N = lines.division(kk);
        loc1 = points.loc(p1,:);
        loc2 = points.loc(p2,:);
        nod(nodkk+(1:N-1),:) = loc1+(1:N-1)'*(loc2-loc1)/N;
        lines.nodid{kk} = [p1 nodkk+(1:N-1) p2];
        nodkk = nodkk + N-1;
    end
    
    % sufrace mesh
    for kk = 1:surfs.no
        tmp = surfs.line(kk,:);
        L1 = tmp(1); L2 = tmp(2); L3 = tmp(3); L4 = tmp(4);
        L1nod = lines.nodid{L1};
        L2nod = lines.nodid{L2};
        L3nod = lines.nodid{L3};
        L4nod = lines.nodid{L4};
        if( surfs.ori(kk,1)*lines.ori(L1) == -1) L1nod = L1nod(end:-1:1); end
        if( surfs.ori(kk,2)*lines.ori(L2) == -1) L2nod = L2nod(end:-1:1); end
        if( surfs.ori(kk,3)*lines.ori(L3) ==  1) L3nod = L3nod(end:-1:1); end
        if( surfs.ori(kk,4)*lines.ori(L4) ==  1) L4nod = L4nod(end:-1:1); end
        M = length(L1nod); N = length(L2nod);
        
        nodtopo = zeros( M,N );
        nodtopo(:,1) = L1nod;
        nodtopo(:,N) = L3nod;
        nodtopo(1,:) = L4nod;
        nodtopo(M,:) = L2nod;
        for jj = 2:N-1
            a1 = nod(L4nod(jj),:);
            a2 = nod(L2nod(jj),:);
            a = a2-a1;
            for ii = 2:M-1
                b1 = nod(L1nod(ii),:);
                b2 = nod(L3nod(ii),:);
                b = b2-b1;
                c = b1-a1;
                t = c(1)*b(2)-c(2)*b(1);
                t = t/(a(1)*b(2)-a(2)*b(1));
                nod(nodkk+1,:) = a1+t*a;
                nodkk = nodkk + 1;
                nodtopo(ii,jj) = nodkk;
            end
        end
        
        for jj = 1:N-1
            for ii = 1:M-1
                ele(elekk+1,:) = [nodtopo(ii,jj),nodtopo(ii+1,jj),nodtopo(ii+1,jj+1),nodtopo(ii,jj+1)];
                elekk = elekk+1;
            end
        end
    end
    nod = nod(1:nodkk,:);
    ele = ele(1:elekk,:);
    figure(1); hold on;
    patch('Faces',ele,'Vertices',nod,'facecolor','g');
    figure(2); hold on;
    for ii = 1:lines.no
        tmp = points.loc(lines.point(ii,:),:);
        if lines.used(ii) == 1
            plot(tmp(:,1),tmp(:,2),'bo-','linewidth',2);
            mid = (tmp(1,:)+tmp(2,:))/2;
            text(mid(1),mid(2),num2str(ii),'color','r'); 
        else
            plot(tmp(:,1),tmp(:,2),'g-','linewidth',1);
        end
    end
    save(file,'nod','ele','lines');
end

Created file 'C:\Users\RenLi\__model_cochlea\cochlea_model_2d_create_mesh.m'.

%plot inline --size 1500,300
cochlea_model_2d_create_mesh('mesh.mat');

The function cochlea_model_2d_passive_finite_difference.m calculate the problem with finite element method

%%file cochlea_model_2d_passive_finite_element.m
function [nod,ele,P,Pup,Pdn,U] = cochlea_model_2d_passive_finite_element(freq)
load('mesh.mat');
omega = 2*pi*freq;
c = 1430; rho=1000;
Ustapes = 1;

bc1 = lines.nodid{8}';
bc1 = [bc1 0*bc1];
bc2 = lines.nodid{9}';
bc2tmp = zeros(length(bc2)-1,3);
for ii = 1:length(bc2)-1
    bc2tmp(ii,1) = bc2(ii);
    bc2tmp(ii,2) = bc2(ii+1);
    bc2tmp(ii,3) = -rho*omega^2*Ustapes;
end
bc2 = bc2tmp;

% coupled bc
doline = lines.nodid{2}'; doline = doline(end:-1:1);
upline = lines.nodid{3}';
bc3tmp_1 = zeros(length(upline)-1,6);
for ii = 1:size(bc3tmp_1,1)
    bc3tmp_1(ii,1) = upline(ii);   % n1sv
    bc3tmp_1(ii,2) = upline(ii+1); % n2sv
    bc3tmp_1(ii,3) = doline(ii);   % n1st
    bc3tmp_1(ii,4) = doline(ii+1); % n2st
    x = nod(upline(ii),1);
    stiffness = 2e10*exp(-270*x);
    mass      = 1.5;
    damping   = 2*0.02*sqrt(stiffness*mass);
    Z1        = stiffness-mass*omega^2+1i*omega*damping;
    x = nod(upline(ii+1),1);
    stiffness = 2e10*exp(-270*x);
    mass      = 1.5;
    damping   = 2*0.02*sqrt(stiffness*mass);
    Z2        = stiffness-mass*omega^2+1i*omega*damping;
    bc3tmp_1(ii,5) = Z1;
    bc3tmp_1(ii,6) = Z2;
end
bc3 = bc3tmp_1;
Z = zeros(length(upline),1);
for ii = 1:length(upline)
    x = nod(upline(ii),1);
    stiffness = 2e10*exp(-270*x);
    mass      = 1.5;
    damping   = 2*0.02*sqrt(stiffness*mass);
    Z(ii)     = stiffness-mass*omega^2+1i*omega*damping;
end

% the main program
[nnod,ndim] = size(nod);
[nele,etyp] = size(ele);
space = nele*etyp^2;
fprintf(1,'number of unknowns:              %10d\n',nnod);
fprintf(1,'elements in the stiffness matrix:%10d\n',space);
space = floor(space*2);

% gauss integral set up
gauss2 = [ -0.577350269189626 0.577350269189626];
weight2= [ 1.0000000000000000 1.000000000000000];
for ii = 1:2
for jj = 1:2
    xi = gauss2(ii);
    et = gauss2(jj);
    W_all(:,ii,jj)   =[ 0.25*(xi-1)*(et-1);
                       -0.25*(xi+1)*(et-1);
                        0.25*(xi+1)*(et+1);
                       -0.25*(xi-1)*(et+1) ];
    Wxi_all(:,ii,jj) =[ 0.25*(et-1);
                       -0.25*(et-1);
                        0.25*(et+1);
                       -0.25*(et+1) ];
    Wet_all(:,ii,jj) =[ 0.25*(xi-1);
                       -0.25*(xi+1);
                        0.25*(xi+1);
                       -0.25*(xi-1) ];
    Weight_all(ii,jj)= weight2(ii)*weight2(jj);  
end
end
% assemble
coe = 1i*omega/c^2;
Kidx  = zeros(space,1);
Kjdx  = zeros(space,1);
Ktmp  = zeros(space,1); Kflag = 0;
Ftmp  = zeros(nnod,1);
for ee = 1:nele
    elee = ele(ee,:);
    node = nod(elee,:);
    Ke = zeros(etyp,etyp); De = Ke; Me = Ke;
    Fe = zeros(etyp,1);
    for ii = 1:2
        for jj = 1:2
            W(:,1)=W_all(:,ii,jj);
            Wxi(:,1)=Wxi_all(:,ii,jj);
            Wet(:,1)=Wet_all(:,ii,jj);
            xy_xiet = node'*[Wxi,Wet];
            jacobi = det(xy_xiet);
            xiet_xy = inv(xy_xiet);
            A = [Wxi Wet]*xiet_xy;
            Wx = A(:,1);Wy = A(:,2);
            De = De + jacobi*Weight_all(ii,jj)*(Wx*Wx'+Wy*Wy');
            Me = Me + jacobi*Weight_all(ii,jj)*(W*W');
            Fe = Fe + 0; % no body force
            Ke = Ke + De + coe*Me;
        end
    end
    list    = elee';
    Kidx(Kflag+1:Kflag+etyp^2) = [list;list;list;list];
    Kjdx(Kflag+1:Kflag+etyp^2) = [list list list list]';
    Ktmp(Kflag+1:Kflag+etyp^2) = Ke(:); Kflag = Kflag + etyp^2;
    Ftmp(list) = Ftmp(list) + Fe(:);
end
% 2rd class boundry conditions
for ii = 1:size(bc2,1)
    n1 = bc2(ii,1); n2 = bc2(ii,2);
    h  = bc2(ii,3);
    xy1 = nod(n1,:); xy2 = nod(n2,:); L = norm(xy2-xy1);
    Fe = h*[0.5;0.5]*L;
    list = [n1;n2];
    Ftmp(list) = Ftmp(list)+Fe(:);
end
% 3rd class boundry conditions / special for bm
for ii = 1:size(bc3,1)
    n1sv = bc3(ii,1); n2sv = bc3(ii,2);
    n1st = bc3(ii,3); n2st = bc3(ii,4);
    Z1 = bc3(ii,5); Z2 = bc3(ii,6);
    % for the SV part
    xy1 = nod(n1sv,:); xy2 = nod(n2sv,:); L = norm(xy1-xy2);
    Ke = [2,1;1,2]/6*L*rho*omega^2*[1/Z1,-1/Z1,0,0; 0,0, 1/Z2,-1/Z2];
    Kidx(Kflag+1:Kflag+8) = [n1sv n2sv n1sv n2sv n1sv n2sv n1sv n2sv];
    Kjdx(Kflag+1:Kflag+8) = [n1st n1st n1sv n1sv n2st n2st n2sv n2sv];
    Ktmp(Kflag+1:Kflag+8) = Ke(:); Kflag = Kflag + 8;
    % for the ST part
    xy1 = nod(n1st,:); xy2 = nod(n2st,:); L = norm(xy1-xy2);
    Ke = -[2,1;1,2]/6*L*rho*omega^2*[1/Z1,-1/Z1,0,0; 0,0, 1/Z2,-1/Z2];
    Kidx(Kflag+1:Kflag+8) = [n1st n2st n1st n2st n1st n2st n1st n2st];
    Kjdx(Kflag+1:Kflag+8) = [n1st n1st n1sv n1sv n2st n2st n2sv n2sv];
    Ktmp(Kflag+1:Kflag+8) = Ke(:); Kflag = Kflag + 8;
end
Kstiff = sparse( Kidx(1:Kflag), Kjdx(1:Kflag), Ktmp(1:Kflag), nnod,nnod);
F      = Ftmp;

% 1rd class boundary conditions
dbc = bc1;
largevalue              = 1.0e8;
indexI                  = zeros(size(dbc,1),1);
KBCtmp                  = zeros(size(dbc,1),1);
Kdiag                   = diag(Kstiff);
Kii                     = Kdiag(dbc(:,1));
for ii = 1:size(dbc,1)
    bcdofs              = dbc(ii,1);
    bcvalu              = dbc(ii,2);
    indexI(ii)          = bcdofs;
    KBCtmp(ii)          = -Kii(ii) + Kii(ii) * largevalue;
end
F(dbc(:,1),1) = largevalue*Kii.*dbc(:,2);
KBC = sparse(indexI,indexI,KBCtmp,size(Kstiff,1),size(Kstiff,2) );
Kstiff = Kstiff + KBC;

% solver
P = full(Kstiff\F);
Pup = P(upline);
Pdn = P(doline);
U   = (Pdn-Pup)./Z;
end

Created file 'C:\Users\RenLi\__model_cochlea\cochlea_model_2d_passive_finite_element.m'.

%plot inline --size 1500,300
[nod,ele,P,Pup,Pdn,U]=cochlea_model_2d_passive_finite_element(1000);
figure(1); patch('Faces',ele,'Vertices',nod,'FaceVertexCData',real(P),'FaceColor','interp','edgecolor','none'); 
title('real(P),1kHz'); colormap('hsv')
figure(2); patch('Faces',ele,'Vertices',nod,'FaceVertexCData',abs(P),'FaceColor','interp','edgecolor','none'); 
title('abs(P),1kHz'); colormap('hsv')
figure(3); plot(linspace(0,1,length(U)),real(U),'r-','linewidth',2); hold on;
plot(linspace(0,1,length(U)), abs(U),'k-','linewidth',2);
plot(linspace(0,1,length(U)),-abs(U),'k-','linewidth',2);

number of unknowns:                    5758
elements in the stiffness matrix:     83520

%plot inline --size 1500,300
[nod,ele,P,Pup,Pdn,U]=cochlea_model_2d_passive_finite_element(500);
figure(1); patch('Faces',ele,'Vertices',nod,'FaceVertexCData',real(P),'FaceColor','interp','edgecolor','none'); 
title('real(P),1kHz'); colormap('hsv')
figure(2); patch('Faces',ele,'Vertices',nod,'FaceVertexCData',abs(P),'FaceColor','interp','edgecolor','none'); 
title('abs(P),1kHz'); colormap('hsv')
figure(3); plot(linspace(0,1,length(U)),real(U),'r-','linewidth',2); hold on;
plot(linspace(0,1,length(U)), abs(U),'k-','linewidth',2);
plot(linspace(0,1,length(U)),-abs(U),'k-','linewidth',2);

number of unknowns:                    5758
elements in the stiffness matrix:     83520

%plot inline --size 1500,300
figure(1); 
for freq = [250,500,1000,2000,4000,8000]
    [nod,ele,P,Pup,Pdn,U]=cochlea_model_2d_passive_finite_element(freq);
    figure(1)
    plot(linspace(0,1,length(U)),real(U),'r-','linewidth',2); hold on;
    plot(linspace(0,1,length(U)), abs(U),'k-','linewidth',2);
    plot(linspace(0,1,length(U)),-abs(U),'k-','linewidth',2);
end
grid on; 
xlabel('Distance from the stapes, %');
ylabel('BM displacement re Stapes');

number of unknowns:                    5758
elements in the stiffness matrix:     83520
number of unknowns:                    5758
elements in the stiffness matrix:     83520
number of unknowns:                    5758
elements in the stiffness matrix:     83520
number of unknowns:                    5758
elements in the stiffness matrix:     83520
number of unknowns:                    5758
elements in the stiffness matrix:     83520
number of unknowns:                    5758
elements in the stiffness matrix:     83520